Как рассчитать прочность армирования по ветровой нагрузке

Основной задачей армирующего профиля, является его сопротивление изгибу и скручиванию. Количественным показателем сопротивления армирующего профиля изгибу является не столько толщина стального листа, из которого изготовлен профиль, не только конфигурация или форма профиля, а в большей степени, момент инерции сечения профиля и модуль упругости материала армирующего профиля. Чем больше момент инерции сечения профиля и модуль упругости материала, из которого он изготовлен, тем выше сопротивление изгибу профиля.

Модуль упругости, (модуль Юнга), кратко Е-модуль, является величиной, зависящей от свойств самого материала. Модуль упругости это та величина нагрузки, при которой стержень из данного материала удлиняется (без потери упругих свойств) вдвое по отношению к ненагруженному образцу. Таким образом, Е-модуль является величиной, характеризующей способность профиля сопротивляться упругой деформации. Величина модуля упругости измеряется в Паскалях (Па). В таблице приведены Е-модули различных материалов, используемых при производстве окон:

Материал	E, H/м2 x l06
ПВХ твердый	2 700
Дерево	10 000
Алюминий	70 000
Сталь	210 000

Из-за маленького значения Е-модуля ПВХ профили должны усиливаться. Из приведённой выше таблицы видно, что оптимальным материалом для профиля, увеличивающего жёсткость, является сталь. Большая разница жесткостей ПВХ и стали является причиной того, что при расчетах на силовые нагрузки, жесткостью ПВХ пренебрегают.

Момент инерции, в отличие от модуля упругости, зависит не от материала, из которого изготовлен профиль, а от его геометрических размеров, формы и конфигурации. Это скалярная физическая величина, характеризующая распределение масс в теле, равная сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Существует несколько видов моментов инерции. Нас интересует геометрический момент инерции. Геометрический момент инерции — геометрическая характеристика сечения, пропорциональная площади сечения и квадратно пропорциональная расстоянию до этого сечения. Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости и взаимного расположения различных элементов конструкции. Значения моментов инерции армирующих профилей, рекомендованных производителем ПВХ профиля, указываются, как правило, в предоставляемой изготовителю окон технической документации. Солидные европейские производители ПВХ профиля предлагают набор из нескольких видов армирующего профиля, предназначенных для использования в условиях различных ветровых нагрузок. Величина момента инерции измеряется в сантиметрах в четвёртой степени (см⁴).

Момент инерции сечения армирующего профиля можно рассчитать и самостоятельно. Сначала определяют точку пересечения координатных осей. Точкой пересечения координатных осей, при определении момента инерции, является общий геометрический центр площадей сечения профиля или центр масс сечения профиля. В замкнутых профилях прямоугольного или круглого сечения, точка пересечения координатных осей, находится в их геометрическом центре. Для определения общего геометрического центра площадей сечения профилей сложной формы, необходимо условно разделить сечение на элементы, определить геометрические центры площадей каждого элемента в отдельности, а затем, определить общий геометрический центр площадей сечения профиля.

Площадь прямоугольных и параллелограммных элементов определяют по формуле:
S_Эл.=Lt;

Смещение геометрического центра площадей относительно габаритов элемента:
h_Эл=L/2; h_Эл=t/2;
Где L – длина элемента, t – толщина стенки элемента.

Площадь радиусных элементов определяют по формулам:
Кольца: S_Эл=π(R²-r²);
Полукольца: S_Эл=π(R²-r²)/2;
Четверти кольца: S_Эл=π(R²-r²)/4;

Смещение геометрического центра площадей относительно центра окружности:
Полукольца: h_Эл=4(R³-r³)/3π(R²-r²);
Четверти кольца: h_Эл=4(R³-r³)/3π√2(R²-r²);
Где R – наружный радиус кольца, r – внутренний радиус кольца.

Определив общий геометрический центр площадей элементов сечения профиля, принимаем его за центр координат при определении момента инерции сечения профиля.

Для определения момента инерции сечения профиля сложной формы, необходимо разделить сечение на элементы простой формы, определить моменты инерции каждого элемента и сложить полученные результаты. Если элемент делится на части осью координат, момент инерции каждой части элемента рассчитывается отдельно, результаты вычислений складываются.

Момент инерции прямоугольных элементов, примыкающих к оси координат под прямым углом, рассчитывается по формуле:
I_Эл=L³t/3;
Где L – длина элемента, t – толщина стенки элемента.

Момент инерции параллелограммных элементов, примыкающих к оси координат под непрямым углом, рассчитывается по формуле:
I_Эл=Н³t/3cosα;
Где Н – высота элемента, по отношению к оси координат, t – толщина стенки элемента, α – угол отклонения от прямого угла между элементом и осью координат.
Или
I_Эл=Н³t/3sinα;
Где Н – высота элемента, по отношению к оси координат, t – толщина стенки элемента, α – угол между элементом и осью координат.

Момент инерции прямоугольных элементов, параллельных оси координат и отстоящих от неё на расстоянии H, рассчитывается по формуле:
I_Эл=L((H+t) ³-H³)/3;
Где L – длина элемента, t – толщина стенки элемента, Н – расстояние от элемента до оси координат.

Момент инерции параллелограммных элементов, находящихся под непрямым углом к оси координат и отстоящих от неё на расстоянии Н, рассчитывается по формуле:
I_Эл= (2BH³-2Bh³-3Bh(H-h) ²-2B(H-h-t/cosα) ³-3Bh(H-h-t/cosα) ²)/6;
Где В – длина проекции элемента на ось координат, h - высота элемента, Н - высота элемента, по отношению к оси координат, t – толщина стенки элемента, α – угол между элементом и осью координат.
Или
I_Эл=(2LH³cosα-2Lh³cosα-3Lh(H-h) ²cosα-2L(H-h-t/cosα) ³cosα-3Lh(H-h-t/cosα) ²cosα)/6;
Где L – длина элемента, h - высота элемента, Н - высота элемента, по отношению к оси координат, t – толщина стенки элемента, α – угол между элементом и осью координат.

Моменты инерции радиусных элементов определяются по формулам:
Кольца: I_Эл=π(R²-r²)Н²+π(D⁴-d⁴)/64;

Если центр окружности элемента находится между элементом и осью координат:
Полукольца: I_Эл=(π(R²-r²)/2)(Н+4(R³-r³)/3π(R²-r²))²+π(D⁴-d⁴)/128;
Четверти кольца: I_Эл=(π(R²-r²)/4)(Н+4(R³-r³)/3π√2(R²-r²))²+π(D⁴-d⁴)/256;

Если центр окружности элемента находится за элементом от оси координат:
Полукольца: I_Эл=(π(R²-r²)/2)(Н-4(R³-r³)/3π(R²-r²))²+π(D⁴-d⁴)/128;
Четверти кольца: I_Эл=(π(R²-r²)/4)(Н-4(R³-r³)/3π√2(R²-r²))²+π(D⁴-d⁴)/256;
Где D – наружный диаметр кольца, d – внутренний диаметр кольца, R – наружный радиус кольца, r – внутренний радиус кольца, Н – расстояние от центра окружности элемента до оси координат.

Момент инерции треугольника с основанием B и высотой H относительно оси проходящей через основание:
I_Эл=BH³/12;

Момент инерции треугольника, с основанием параллельным оси координат и вершиной на самой оси:
I_Эл=BH³/4;
Где B – основание треугольника, параллельное оси координат; Н – высота треугольника, перпендикулярная оси координат.

Каждая конструкция из ПВХ профиля, будь то окно, балконная дверь, балконное остекление, или любое другое изделие, на этапе проектирования или конструирования, должны быть рассчитаны на сопротивление ветровым нагрузкам, которым они будут подвержены в течение срока эксплуатации. Это называется статический расчёт строительного элемента. Он имеет своей целью привести доказательство того, что элемент с заданной надёжностью выдержит действующие на него нагрузки без остаточных деформаций и разрушения. При этом все действующие на окно силы, должны быть переданы на несущие элементы здания. Достаточность прочности профиля определяется величиной прогиба, вызванного ветровой нагрузкой, собственным весом элементов окна и другими нагрузками.


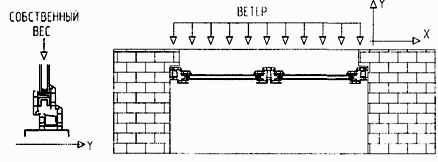На рисунке показаны направления основных сил, воздействующих на окно.

Максимально допустимый прогиб окон и балконных дверей, под действием расчётных ветровых нагрузок, согласно ДСТУ Б В. 2. 6 – 15 - 99 «Конструкции зданий и сооружений. Окна и двери поливинилхлоридные. Общие технические условия», при длине элементов до трёх метров, не должен превышать 1/200 длины прогона. Для изделий, размером свыше трёх метров (по индивидуальным заказам), прогиб должен быть не больше 1/300 длины прогона, причём в конструкциях, застеклённых стеклопакетами, - не более 8 мм на каждый стеклопакет. Немецкие нормы более требовательны, Допустимые деформации немецких профилей определяются согласно DIN 18056 "Стены с окнами, измерения и исполнения". Согласно этим нормам, допустимая деформация для импоста и поперечного профиля прямоугольного к поверхности окна не может быть более 1/300 профильной длины, 0,8 см для стеклопакета с длиной стороны более 240 см.

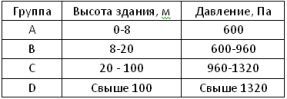
Приведу основные положения расчета на ветровые нагрузки в соответствии с немецкими нормами DIN, поскольку на сегодняшний день эта методика является наиболее простой, понятной и широко применяемой российскими и украинскими фирмами. Кроме того, значения ветровых нагрузок согласно DIN 1055, более жёсткие, чем по ДБН В.1.2-2:2006. Согласно DIN 1055 ветровая нагрузка, в зависимости от высоты здания, подразделяется на четыре группы:


Согласно ДБН В.1.2-2:2006 «Система обеспечения надёжности и безопасности строительных объектов. Нагрузки и воздействия. Нормы проектирования», расчёт ветровых нагрузок более сложный, но позволяющий более точно определить величину ветровой нагрузки с учётом к специфичным условиям местности, в которой расположен объект остекления. Предельное расчетное значение ветровой нагрузки определяется по формуле:

W_m=γ_fmW₀C;
где γ_fm– коэффициент надёжности по предельному значению ветровой нагрузки определяется в зависимости от периода повторяемости. Для объектов массового строительства, допускается средний период повторяемости принимать равным установленному сроку эксплуатации сооружения. При сроке эксплуатации равном 50 годам, γ_fm равен одинице.
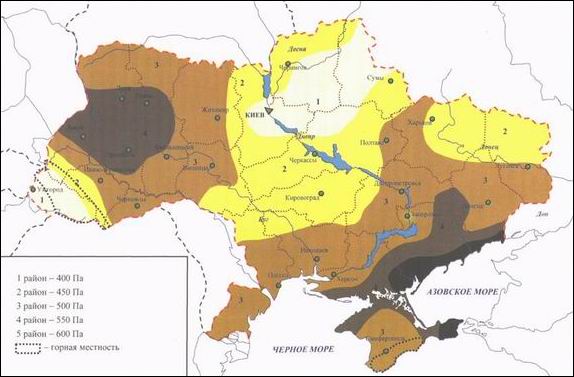
W₀ – характеристическое значение ветрового давления, равное средней (статистической) составляющей давления ветра на высоте 10 м, которое может быть превышено, в среднем, один раз в пятьдесят лет, определяемое, в зависимости от ветрового района по карте или по приложению Е ДБН В.1.2-2:2006.



С – коэффициент, упрощённо, определяемый по формуле:

С = C_h C_alt C_rel C_dir C_d;
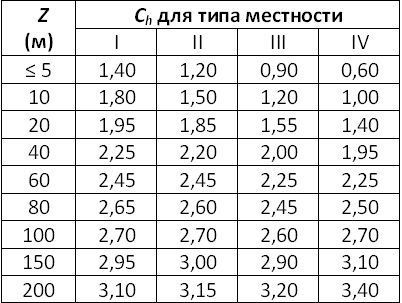
Где C_h – коэффициент высоты сооружения, учитывающий увеличение ветровой нагрузки, в зависимости от высоты сооружения или его рассматриваемой части над поверхностью земли (Z), типа окружающей местности. Типы местности, окружающие здание или сооружение, определяются для каждого расчётного направления ветра в отдельности:


I – открытые поверхности морей, озёр, а также плоские равнины без препятствий, подвергающиеся действию ветра на участке более 3 км;
II – сельская местность с оградами (заборами), небольшими сооружениями, домами и деревьями;
III – пригородные и промышленные зоны, протяжённые лесные массивы;
IV – городские территории, на которых по крайней мере 15% поверхности заняты зданиями, имеющими среднюю высоту более 15 м.

При определении типа местности сооружение считается расположенным на местности данного типа для определённого расчётного направления ветра, если в рассматриваемом направлении такая местность имеется на расстоянии 30Z при полной высоте сооружения Z<60 м или 2 км при большей высоте. В случае если сооружение на границе местностей различного типа либо имеются сомнения относительно выбора типа местности, следует принимать тип местности, обеспечивающий большее значение коэффициента C_h. Коэффициент C_h определяют по таблице. Промежуточные значения коэффициента C_h определяют линейной интерполяцией.

C_alt – коэффициент географической высоты учитывает высоту Н (в километрах) размещения строительного объекта над уровнем моря и определяется по формуле:
C_alt = 2H (H > 0,5 км);
C_alt = 1 (H ≤ 0,5 км);

C_rel – коэффициент рельефа, учитывающий микрорельеф местности вблизи площадки, на которой расположен строительный объект. Коэффициент рельефа принимается равным единице, за исключением случаев, когда объект строительства расположен на холме или склоне. Коэффициент рельефа следует учитывать в том случае, когда сооружение расположено на холме или склоне на расстоянии от начала склона не менее чем половина длины склона или полторы высоты холма. Коэффициент рельефа определяется по формулам:
C_rel = 1 при φ <0.05;
C_rel = 1 + 2Sφ при 0.05 < φ <0.3;
C_rel = 1 + 0.6 при φ > 0.3;
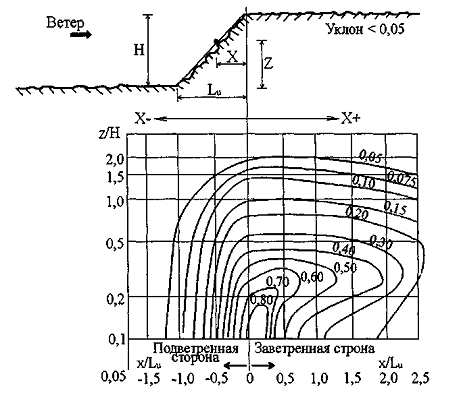
Где φ - уклон с заветренной стороны; S – коэффициент, определяемый по рисункам для склонов и холмов.


Коэффициент S для склонов.


Коэффициент S для холмов.

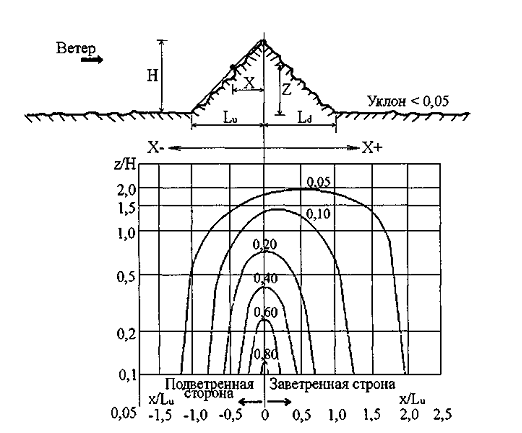На рисунках обозначено:
φ - уклон H/L с заветренной стороны; Lu – проекция длины подветренного склона на горизонталь; Ld – проекция длины заветренного склона на горизонталь; Н – высота холма или склона; Х – расстояние по горизонтали от сооружения до вершины; Z – расстояние по вертикали от поверхности земли до сооружения; L_e – эффективная длина подветренного склона (L_e=L при 0,05< φ <0,3; L_e=3,3H при φ >0,3).

C_dir – коэффициент направления учитывает неравномерность ветровой нагрузки и, как правило, принимается равным единице. Значение C_dir, отличное от единицы, допускается учитывать при специальном обосновании только для открытой равнинной местности и при наличии значительных статистических данных.

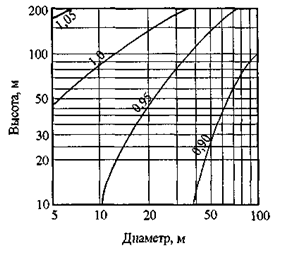
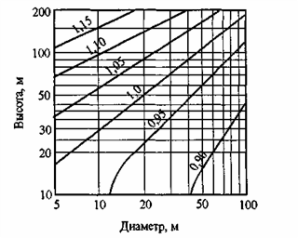
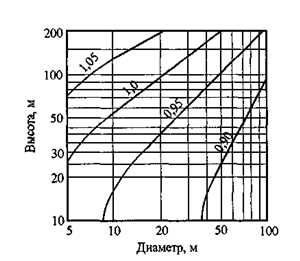
C_d – коэффициент динамичности учитывает влияние пульсационной составляющей ветровой нагрузки и пространственную корреляцию ветрового давления на сооружение. Для основных типов зданий и сооружений значения C_d определяются по графикам. Указанные на рисунках ширина и диаметр приняты в сечении, перпендикулярном ветровому потоку. Значения C_d следует принимать по левой кривой соответствующего графика.

Для каменных зданий и зданий с ж/б каркасом.

Для зданий со стальным каркасом.

Для зданий со сталебетонным каркасом.

Поскольку рама достаточно жёстко крепится в проёме, статический расчёт, в основном, проводится для импостов. Если по каким-либо причинам не выполняется условие по максимальному расстоянию между точками крепления 700 мм, то производится и расчёт свободной длины профиля рамы, аналогично расчёту импоста.

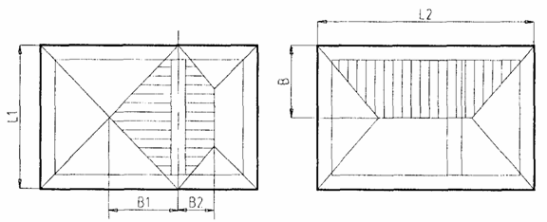
Распределение давления воздушного потока, действующего в качестве плоскостной нагрузки на окно, осуществляется через биссектрису угла в соответствии с изображениями на рисунках. При распределении нагрузок под углом 45^˚, в квадрате образуются четыре треугольные поверхности, а в прямоугольнике - две треугольные и две трапециевидные. Для определения размера в треугольной или трапециевидной нагрузки делится пополам самая короткая сторона. При этом нагрузка на раму приходит с одной поверхности, а на импост или стык блоков - с обеих соприкасающихся поверхностей.



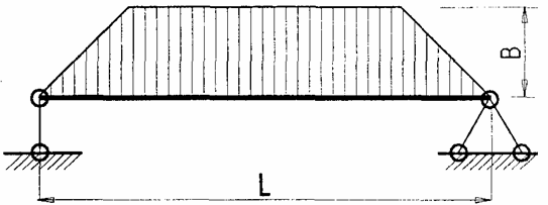
Предполагается, что рама состоит из отдельных образующих ее вертикальных и горизонтальных элементов, шарнирно соединенных между собой. При этом каждый отдельный элемент, подвергающийся воздействию ветровой нагрузки, рассматривается как шарнирно опертая балка на двух опорах, нагруженная равномерно распределенной нагрузкой. Такая схема соответствует конструкции металлопластиковой оконной рамы (и створки), в которой не предполагается жесткой связи между армирующими стальными элементами (причина - в значительном удешевлении за счет этого технологии изготовления окон). Хотя соединение профилей импостов с рамой обеспечивает некоторую жёсткость заделки, для увеличения надёжности при расчётах это не учитывается.



Формула для расчёта необходимого момента инерции для обеспечения допустимого прогиба при заданных размерах окна и ветровой нагрузки:
I_x=wL⁴B(25-40(B/L) ²+16(B/L) ⁴)/1920Ef см⁴;
Где w – давление ветра (Н/мм²); B – ширина эпюры нагружения (см); L – длина профиля (см); E – Е-модуль (Н/мм²); f – максимально допустимый прогиб (см).

Таким образом, можно рассчитать требуемое значение момента инерции.

Для определения прогиба профиля заданной жёсткости и длины под действием известной ветровой нагрузки пользуются следующей формулой:
f=wL⁴B(25-40(B/L)²+16(B/L) ⁴)/1920EI_x см;
Где w – давление ветра (Н/мм²); B – ширина эпюры нагружения (см); L – длина профиля (см); E – Е-модуль (Н/мм²); I_x – момент инерции (см⁴).